Recall: A key metric for evaluating model performance

Measuring the performance of ML models is crucial, and the ML evaluation metric – Recall – holds a special place, especially when the cost of missing a positive instance is high. In this guide, we will delve into the nitty-gritty of Recall. We will explore why it’s vital in certain applications like medical diagnostics and fraud detection and how it fits into the production lifecycle of ML systems.

Understanding Recall

What is Recall (True Positive Rate)?

Recall, also known as Sensitivity or the True Positive Rate, is a metric that measures the ability of a model to correctly identify all the relevant instances. In simple terms, it tells us what proportion of actual positives our model correctly identified.

Recall formula

The formula for Recall is:

Recall = True Positives / (True Positives + False Negatives)

Example with a simple confusion matrix

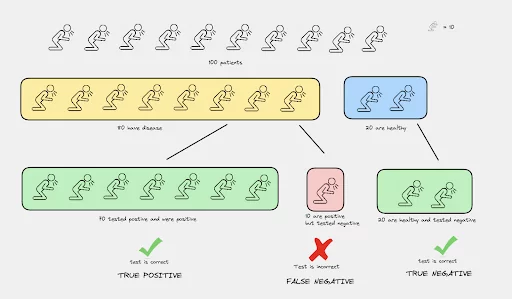
Let’s take an example. Imagine a medical test to detect a disease. In this scenario:

• True Positives (TP): People who have the disease and tested positive.
• False Negatives (FN): People who have the disease but tested negative.

Let’s say out of 100 patients, 80 have the disease. The test identified 70 patients correctly but missed 10. Here, TP = 70, and FN = 10.

Using the formula:

Recall = 70 / (70+10) = 0.875

This tells us that the test was able to correctly identify 87.5% of the patients with the disease.

Here is an example where we compute some commonly used metrics in a binary classification problem, given the values for True Positives (TP) and False Negatives (FN):

# Given values
TP = 70  # True Positives
FN = 10  # False Negatives

# Total number of actual positives
P = TP + FN

# Sensitivity, hit rate, recall, or true positive rate (TPR)
sensitivity = TP / P
print("Sensitivity (Recall or True Positive Rate): ", sensitivity)

# Miss rate or False Negative Rate (FNR)
miss_rate = FN / P
print("Miss Rate (False Negative Rate): ", miss_rate)

# Precision or Positive Predictive Value (PPV)
# Assuming True Negatives (TN) and False Positives (FP) for completeness.
# These are not given in the problem so we'll set them to hypothetical values.
TN = 20  # True Negatives (people without disease tested negative)
FP = 0  # False Positives (people without disease tested positive)
precision = TP / (TP + FP)
print("Precision (Positive Predictive Value): ", precision)

This script assumes that there were no False Positives (i.e., people without the disease who were incorrectly identified as having it), as that information wasn’t provided in the original problem. In real-world scenarios, you’d also want to calculate metrics like the False Positive Rate (FPR) and the overall accuracy of the model, but those would require knowing the number of True Negatives (TN) and False Positives (FP) as well.

Differentiating Recall from Precision

While Recall focuses on minimizing false negatives, Precision focuses on minimizing false positives. Precision is defined as:

Precision = True Positives / (True Positives + False Positives)

Understanding Accuracy 

What is Accuracy?

Accuracy is another key metric in evaluating the performance of classification models. It is defined as the proportion of all true predictions (both positive and negative) over all predictions. It provides an overall measure of how often the model is correct, regardless of whether the instance is positive or negative.

Accuracy Formula

The formula for Accuracy is:

Accuracy = (True Positives + True Negatives) / (True Positives + True Negatives + False Positives + False Negatives)

Example with a Simple Confusion Matrix

Continuing with our previous example of a medical test to detect a disease, we have:

True Positives (TP): 70 patients who have the disease and tested positive.
False Negatives (FN): 10 patients who have the disease but tested negative.
True Negatives (TN): 20 patients who don’t have the disease and tested negative.
False Positives (FP): 0 patients who don’t have the disease but tested positive.

Using the formula:

Accuracy = (70 + 20) / (70 + 20 + 0 + 10) = 0.9

This tells us that the test was correct 90% of the time.

Relationship Between Accuracy, Recall, and Precision 

While Accuracy provides an overall measure of model correctness, Recall and Precision focus on how well the model performs in positive instances.

Recall measures the ability of a model to identify all relevant instances or how many of the actual positives our model can capture. In contrast, Precision focuses on how many of the predicted positives are actually positive.

Let’s consider two extreme scenarios:

1. A model that labels all instances as positive will have a perfect Recall of 1.0 because it doesn’t miss any positive instance. However, this model will have poor Precision because it falsely classifies many negatives as positives, thereby decreasing its Precision.
2. Conversely, a model that labels very few instances as positive but is correct whenever it does will have high Precision but low Recall. That’s because it misses many actual positive instances.

Accuracy is a more holistic measure as it takes both True Positives and True Negatives into account. However, in situations where the classes are imbalanced, or the cost of misclassifying positives is very high, one might prefer to use Recall or Precision, or a combination of both like the F1 score.

Let’s get practical for a second and consider a dataset with 100 instances, 95 negative and 5 positive. If a model simply classifies all instances as negative, its Accuracy would be 95/100 = 0.95 or 95%, which seems quite high. However, its Recall would be 0/5 = 0 because it failed to identify any positive instance.

So, Accuracy alone might be misleading when dealing with imbalanced classes, and that’s where Precision and Recall become vital. They provide a more focused view on the performance of the model, particularly on the positive (minority or critical) class.

Recall in the context of classification models

Binary classification & Recall

In binary classification, we are often interested in the performance of our model regarding a particular class – for example, patients with a disease. In such cases, Recall is crucial, particularly when the dataset is imbalanced, i.e., the number of positive samples is much lower than negatives.

Multi-class classification & Recall

In multi-class problems, Recall can be calculated for each class separately by considering one class as positive and the rest as negative. We can then average these Recall values. The two common methods are:

• Micro-averaging: Calculate TP and FN for each class, sum them up, and then calculate recall.
• Macro-averaging: Calculate recall for each class separately and then average them.

Relation between Recall and Sensitivity

Recall is the same as Sensitivity. Both terms are used interchangeably.

Application scenarios for Recall

When Recall is Critical

• Medical Diagnostics: In medical diagnostics, false negatives (a sick patient misclassified as healthy) can be very dangerous. Therefore, high recall is desirable.
• Fraud Detection: In fraud detection, it’s critical to catch as many fraudulent transactions as possible, even if it means sometimes flagging some legitimate transactions.

When Recall may not be the Only Priority

• Email Spam Filtering: In spam detection, you don’t want to have too many false positives (non-spam emails classified as spam).
• Image Recognition: Depending on the context, precision, accuracy or F1-score might be more important.

Trade-off between Recall and Precision

Introducing the Precision-Recall Curve

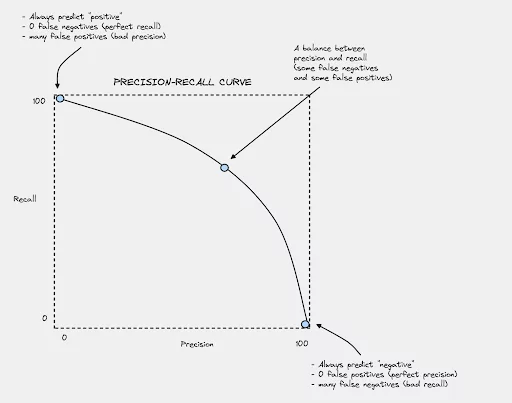
As you try to increase recall by catching more positives, you might end up increasing false positives, which in turn reduces precision. This trade-off can be visualized through the Precision-Recall curve.

F1 Score as the harmonic mean of Precision and Recall

To balance Precision and Recall, we use the F1 score, which is the harmonic mean of Precision and Recall:

F1 = 2 * (Precision * Recall) / (Precision + Recall)

Adjusting classification thresholds to optimize Recall or Precision

By adjusting the threshold of classification, one can optimize for either recall or precision depending on the problem’s requirement.

Practical tips for improving Recall

• Data Sampling Techniques: Use oversampling or SMOTE to handle class imbalance.
• Cost-sensitive Learning: Assign higher costs to misclassifying positive instances.
• Hyperparameter Tuning: Fine-tune the parameters of your algorithm.
• Ensemble Methods: Use ensemble methods to improve recall.

The role of Recall in model evaluation and monitoring 

Recall is critical not just during model development but also during production. Continuous monitoring of Recall can help in identifying concept drift and ensuring that the model continues to perform as expected.

Limitations and Cautions of Recall

• Risks of Over-optimizing Recall: This might make the model biased and less useful.
• Understanding Business Context: Sometimes other metrics may be more critical.
• Importance of Human Evaluation: Particularly in critical applications like healthcare.

Wrapping up recall

We explored what Recall is, its significance, how to compute it, and where it’s critical. While Recall is an essential metric, especially in cases like medical diagnosis, it’s also important not to overlook other metrics that might be critical for a given business context. Understanding and wisely using Recall in production ML systems is crucial.

Or Jacobi